ofPolyline
ofPolyLine allows you to combine multiple points into a single vector data object that can be drawn to the screen, manipulated point by point, and combined with other ofPolyline instances. It is less complex than the ofPath and generally represents a single line or vector shape rather than multiple lines or shapes.
You can add points to an ofPolyline by adding vertices. By default these vertices are ofVec3f types, meaning you also need to specify a z-value, even when drawing in 2D:
float i = 0;
while (i < TWO_PI) { // make a heart
float r = (2-2*sin(i) + sin(i)*sqrt(abs(cos(i))) / (sin(i)+1.4)) * -80;
float x = ofGetWidth()/2 + cos(i) * r;
float y = ofGetHeight()/2 + sin(i) * r;
line.addVertex(ofVec3f(x,y,0));
i+=0.005*HALF_PI*0.5;
}
line.close(); // close the shape
or you can draw lines or curves:
float angle = 0;
while (angle < TWO_PI ) {
b.curveTo(100*cos(angle), 0, 100*sin(angle));
b.curveTo(300*cos(angle), 300, 300*sin(angle));
angle += TWO_PI / 30;
}
ofPolyline also includes methods to get the closest point, determine whether a point is inside shape, and resample shapes. Along with the ofPath class, it's the best way to draw and manipulate 2D and 3D vector graphics that you'll need to update and manipulate frequently.
If you use the lineTo or curveTo or bezierTo functions, you move the drawing point, so that drawing a line to 100,100 means a line from 0,0 to 100, 100. The next line would be a line from 100,100 to wherever you go next. Storing this position means that you can easily create continuous drawings without difficulty.
addVertex( ... )
void addVertex(const T &p)Adds a point using an T at the end of the ofPolyline.
Adds a point using an ofPoint at the end of the ofPolyline.
addVertex( ... )
void addVertex(float x, float y, float z)Adds a point using floats at the end of the ofPolyline.
Adds a point using floats instead of an ofPoint at the end of the ofPolyline.
addVertices( ... )
void addVertices(const T *verts, int numverts)Adds multiple points at the end of the ofPolyline using a pointer to an array of T objects.
Adds multiple points at the end of the ofPolyline using a pointer to an array of ofPoint objects.
ofPoint* verts = new ofPoint[5];
// make a pentagon
float size = 80.f;
float X1 = 0.125*sqrt(10 + 2*sqrt(5)) * size;
float X2 = 0.125*sqrt(10 - 2*sqrt(5)) * size;
float Y1 = 0.125*(sqrt(5) - 1) * size;
float Y2 = 0.125*(sqrt(5) + 1) * size;
verts[0] = ofPoint(0, -0.5 * size);
verts[1] = ofPoint(-X1, -Y1);
verts[2] = ofPoint(-X2, Y2);
verts[3] = ofPoint(X2, Y2);
verts[4] = ofPoint(X1, -Y1);
ofPolyline p;
p.addVertices(verts, 5);
arc( ... )
void arc(const T ¢er, float radiusX, float radiusY, float angleBegin, float angleEnd, int circleResolution=20)Adds an arc around the T center with the width of
radiusX and the height of radiusY.
The angleBegin and angleEnd indicate the start and end angles
of the arc in degrees measured clockwise from the x-axis.
Optionally, you can specify circleResolution, which is the number of
line segments a circle would be drawn with. A partial arc will be
drawn with the same resolution: if circleResolution == 20, a half-
circle will be drawn with 10 segments.
If there are already vertexes in the ofPolyline the arc will extend them; a line will be created from the endmost point on the ofPolyline to the beginning point of the arc.
ofPolyline polyline1, polyline2;
// draw an line, then an semi-circle in red
polyline2.lineTo(300, 50);
T point2(450,120);
polyline2.arc(point2,100,100,0,180);
ofSetColor(ofColor::red);
polyline2.draw();

Draws an arc around the ofPoint center with the width of radiusX and the height of radiusY.
The angleBegin and angleEnd indicate the start and end angles of the arc in degrees measured clockwise from the x-axis.
Optionally, you can specify circleResolution, which is the number of line segments a circle would be drawn with.
A partial arc will be drawn with the same resolution: if circleResolution == 20, a half-circle will be drawn with 10 segments.
If there are already vertices in the ofPolyline the arc will extend them; a line will be created from the endmost point on the ofPolyline to the beginning point of the arc.
Example:
ofPolyline polyline1, polyline2;
// draw an circle with a diameter of 100 in blue
ofPoint point1(150,120);
polyline1.arc(point1,100,100,0,360);
ofSetColor(ofColor::blue);
polyline1.draw();
// draw an line, then an semi-circle in red
polyline2.lineTo(300, 50);
ofPoint point2(450,120);
polyline2.arc(point2,100,100,0,180);
ofSetColor(ofColor::red);
polyline2.draw();

arc( ... )
void arc(const T ¢er, float radiusX, float radiusY, float angleBegin, float angleEnd, bool clockwise, int circleResolution=20)Adds an arc around the T center with the width of radiusX
and the height of radiusY to the polyline.
The angleBegin and angleEnd indicate the start and end angles of
the arc in degrees measured clockwise from the x-axis.
The clockwise boolean sets the drawing direction. Passing 'false' to
it will draw the arc counter-clockwise.
Optionally, you can specify circleResolution, which is the number of
line segments a circle would be drawn with.
If the arc doesn't start at the same point the last vertex finished a straight line will be created to join both
Draws an arc around the ofPoint center with the width of radiusX and the height of radiusY.
The angleBegin and angleEnd indicate the start and end angles of the arc in degrees measured clockwise from the x-axis.
The clockwise boolean sets the drawing direction. Passing 'false' to it will draw the arc counter-clockwise.
Optionally, you can specify circleResolution, which is the number of line segments a circle would be drawn with.
arc( ... )
void arc(float x, float y, float radiusX, float radiusY, float angleBegin, float angleEnd, int circleResolution=20)Adds an arc around the coordinates (x,y) with the width of
radiusX and the height of radiusY.
The angleBegin and angleEnd indicate the start and end angles
of the arc in degrees measured clockwise from the x-axis.
Optionally, you can specify circleResolution, which is the number
of line segments a circle would be drawn with.
Draws an arc around the coordinates (x,y) with the width of radiusX and the height of radiusY.
The angleBegin and angleEnd indicate the start and end angles of the arc in degrees measured clockwise from the x-axis.
Optionally, you can specify circleResolution, which is the number of line segments a circle would be drawn with.
arc( ... )
void arc(float x, float y, float z, float radiusX, float radiusY, float angleBegin, float angleEnd, int circleResolution=20)Adds an arc around the coordinates (x,y,z) with the width of
radiusX and the height of radiusY.
The angleBegin and angleEnd indicate the start and end angles of
the arc in degrees measured clockwise from the x-axis.
Optionally, you can specify circleResolution, which is the number of
line segments a circle would be drawn with.
Draws an arc around the coordinates (x,y,z) with the width of radiusX and the height of radiusY.
The angleBegin and angleEnd indicate the start and end angles of the arc in degrees measured clockwise from the x-axis.
Optionally, you can specify circleResolution, which is the number of line segments a circle would be drawn with.
arcNegative( ... )
void arcNegative(const T ¢er, float radiusX, float radiusY, float angleBegin, float angleEnd, int circleResolution=20)arcNegative( ... )
void arcNegative(float x, float y, float radiusX, float radiusY, float angleBegin, float angleEnd, int circleResolution=20)arcNegative( ... )
void arcNegative(float x, float y, float z, float radiusX, float radiusY, float angleBegin, float angleEnd, int circleResolution=20)bezierTo( ... )
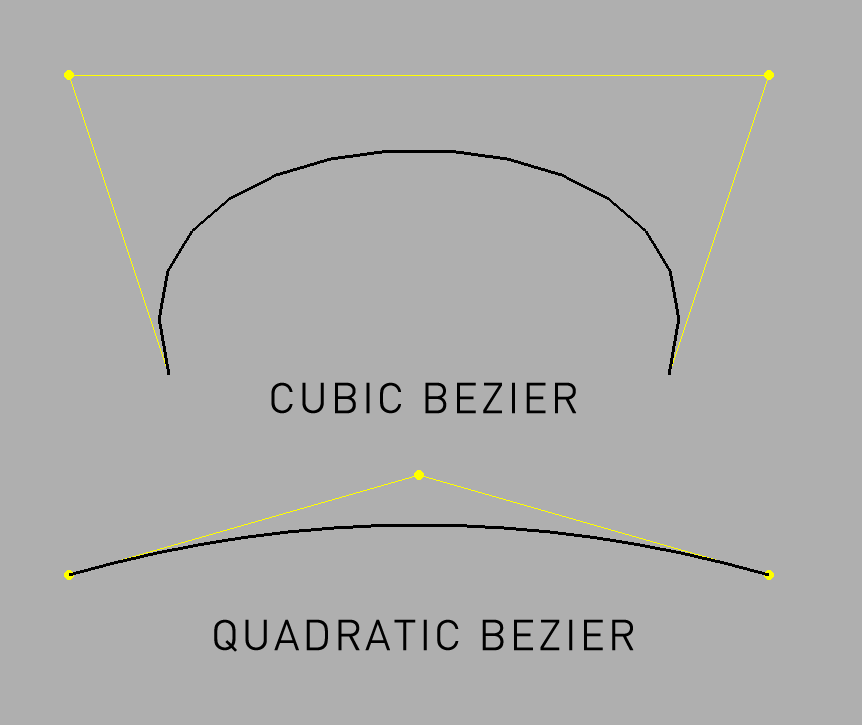
void bezierTo(const T &cp1, const T &cp2, const T &to, int curveResolution=20)Adds a cubic bezier line from the current drawing point with the 2 control points indicated by T cp1 and cp2, that ends at T to.
line.addVertex(T(200, 400));
line.bezierTo(100, 100, 800, 100, 700, 400);
 The control points are shown in red.
The control points are shown in red.
Creates a cubic bezier line from the current drawing point with the 2 control points indicated by ofPoint cp1 and cp2, that ends at ofPoint to. For instance, the following:
line.addVertex(ofPoint(200, 400));
line.bezierTo(100, 100, 800, 100, 700, 400);
Creates this:
 The control points are shown in yellow.
The control points are shown in yellow.
bezierTo( ... )
void bezierTo(float cx1, float cy1, float cx2, float cy2, float x, float y, int curveResolution=20)Adds a cubic bezier line from the current drawing point with the 2 control points indicated by the coordinates cx1, cy1 and cx2, cy2, that ends at the coordinates x, y.
Creates a cubic bezier line from the current drawing point with the 2 control points indicated by the coordinates cx1, cy1 and cx2, cy2, that ends at the coordinates x, y.
bezierTo( ... )
void bezierTo(float cx1, float cy1, float cz1, float cx2, float cy2, float cz2, float x, float y, float z, int curveResolution=20)Adds a cubic bezier line in 3D space from the current drawing point with the 2 control points indicated by the coordinates cx1, cy1, cz1 and cx2, cy2, cz2, that ends at the coordinates x, y, z.
Creates a cubic bezier line in 3D space from the current drawing point with the 2 control points indicated by the coordinates cx1, cy1, cz1 and cx2, cy2, cz2, that ends at the coordinates x, y, z.
float cx = ofGetWidth()/2;
float cy = 200;
float step = TWO_PI / 60;
for (float i = 0.0; i < TWO_PI; i+=step) {
if(i == 0.0) {
line.addVertex(cx + (400*cos(i)), cy+400, 400 * sin(i));
} else {
line.bezierTo( cx - (200*cos(i)), cy-100, 400 * sin(i),
cx + (200*cos(i)), cy+600, 400 * sin(i),
cx + (400*cos(i)), cy+400, 400 * sin(i));
}
}
calcData( ... )
void calcData(int index, T &tangent, float &angle, T &rotation, T &normal)clear( )
void clear()Removes all the points from the ofPolyline.
Removes all the points from the ofPolyline.
close( )
void close()Closes the ofPolyline, meaning that all the vertices will be linked and can be "walked".
Closes the ofPolyline, meaning that all the vertices will be linked and can be "walked".
curveTo( ... )
void curveTo(const T &to, int curveResolution=20)Adds a curve to an T object passed in
float angle = 0;
while (angle < TWO_PI ) {
b.curveTo( T(100*cos(angle), 100*sin(angle)));
b.curveTo( T(300*cos(angle), 300*sin(angle)));
angle += TWO_PI / 30;
}
\note You need at least 4 points to be able to use curveTo()
See also: Catmull-Rom splines wiki
Draws a curve to an ofPoint object passed in:
float angle = 0;
while (angle < TWO_PI ) {
b.curveTo( ofPoint(100*cos(angle), 100*sin(angle)));
b.curveTo( ofPoint(300*cos(angle), 300*sin(angle)));
angle += TWO_PI / 30;
}
You need at least 4 points to be able to draw with curveTo, here's an explanation of why this happens:
If we have an empty ofPolyline p, and we do:
p.lineTo(v0);
p.lineTo(v1);
p.lineTo(v2);
p.lineTo(v3);
We end up with a line that starts at v0, heads to v1, then heads to v2 and finally ends at v3. But if we had instead done:
p.curveTo(v0);
p.curveTo(v1);
p.curveTo(v2);
p.curveTo(v3);
We end up with a curve that goes from v1 to v2. That might seem initially puzzling...
So, we have to dive under the hood. The curveTo(...) method makes Catmull-Rom splines wiki. The relevant bit to understand is that this type of spline is defined by four points:

P1 and P2 are the endpoints of our curve, while P0 and P3 are the control that define the shape of the curve.
When using curveTo(...) with ofPolyline, there's an internal vector that stores P0, P1, P2 and P3. When our ofPolyline is empty then the internal vector is also empty. When we call:
p.curveTo(v0); // Internal vector is [v0], so only P0 is defined
p.curveTo(v1); // Internal vector is [v0, v1], so only P0 and P1 are defined
p.curveTo(v2); // Internal vector is [v0, v1, v2], so only P0, P1 and P2 are defined
p.curveTo(v3); // Internal vector is [v0, v1, v2, v3], so all points are defined
Only once all of those points (P0 through P4) have been defined, then a spline has been fully defined and vertices can finally be added to our ofPolyline. When curveTo(v3) is called above, then the curve between P1 (v1) and P2 (v2) is sampled (at a resolution defined by the optional parameter curveResolution). That sampling slides along the curve and adds vertices to your ofPolyline.
The curve doesn't start at v0 and end at v3 because those points are acting as the control points (i.e. the points connected by dotted lines in the image above).
And now that we have P0 through P4 defined, when we call curveTo(...) next:
curveTo(v4); // Internal vector becomes [v1, v2, v3, v4]
The oldest point, v0, was bumped and everything shifted down. The sampling occurs again, but this time it is between v2 and v3.
curveTo( ... )
void curveTo(float x, float y, float z, int curveResolution=20)Adds a curve to the x,y,z points passed in with the optional resolution.
Draws a curve to the x,y,z points passed in with the optional resolution.
float angle = 0;
while (angle < TWO_PI ) {
polyline.curveTo(100*cos(angle), 0, 100*sin(angle));
polyline.curveTo(300*cos(angle), 300, 300*sin(angle));
angle += TWO_PI / 30;
}
draw( )
void draw()Draw the line using the current renderer
Draw the line using the current renderer.
flagHasChanged( )
void flagHasChanged()getArea( )
float getArea()Gets the precise area bounded by the line
getBoundingBox( )
ofRectangle getBoundingBox()Get the bounding box of the polyline , taking into account all the points to determine the extents of the polyline.
getCentroid2D( )
T getCentroid2D()Get the center of the area bounded by the line
getClosestPoint( ... )
T getClosestPoint(const T &target, unsigned int *nearestIndex)Gets the point on the line closest to the target. You can also optionally pass a pointer to/address of an unsigned int to get the index of the closest vertex
Returns the bounding box of the shape, taking into account all the points to determine the extents of the polyline.
getDegreesAtIndex( ... )
float getDegreesAtIndex(int index)Get angle (degrees) of the path at index
Get the center of the area bounded by the line.
getDegreesAtIndexInterpolated( ... )
float getDegreesAtIndexInterpolated(float findex)Get angle (degrees) at interpolated index (interpolated between neighboring indices)
This returns the point on the line closest to the target. You can also optionally pass a pointer to/address of an unsigned int to get the index of the closest vertex.
getIndexAtLength( ... )
float getIndexAtLength(float f)getIndexAtPercent( ... )
float getIndexAtPercent(float f)getInterpolationParams( ... )
void getInterpolationParams(float findex, int &i1, int &i2, float &t)getLengthAtIndex( ... )
float getLengthAtIndex(int index)Get length along path at index
getLengthAtIndexInterpolated( ... )
float getLengthAtIndexInterpolated(float findex)getNormalAtIndex( ... )
T getNormalAtIndex(int index)Get normal vector at index
getNormalAtIndexInterpolated( ... )
T getNormalAtIndexInterpolated(float findex)Get normal vector at interpolated index (interpolated between neighboring indices)
getPerimeter( )
float getPerimeter()Gets the size of the perimeter of the polyline, good for determining length of the line, rather than just the bounding box shape.
getPointAtIndexInterpolated( ... )
T getPointAtIndexInterpolated(float findex)getPointAtLength( ... )
T getPointAtLength(float f)getPointAtPercent( ... )
T getPointAtPercent(float f)getRadiansAtIndex( ... )
float getRadiansAtIndex(int index)Get angle (degrees) of the path at index
getRadiansAtIndexInterpolated( ... )
float getRadiansAtIndexInterpolated(float findex)Get angle (degrees) at interpolated index (interpolated between neighboring indices)
getRightVector( )
T getRightVector()getRotationAtIndex( ... )
T getRotationAtIndex(int index)Get rotation vector at index (magnitude is sine of angle)
getRotationAtIndexInterpolated( ... )
T getRotationAtIndexInterpolated(float findex)Get rotation vector at interpolated index (interpolated between neighboring indices) (magnitude is sine of angle)
getTangentAtIndex( ... )
T getTangentAtIndex(int index)Get tangent vector at index
getTangentAtIndexInterpolated( ... )
T getTangentAtIndexInterpolated(float findex)Get tangent vector at interpolated index (interpolated between neighboring indices)
getWrappedIndex( ... )
int getWrappedIndex(int index)Get wrapped index depending on whether poly is closed or not
hasChanged( )
bool hasChanged()Returns whether the vertices within the line have changed.
insertVertex( ... )
void insertVertex(const T &p, int index)insertVertex( ... )
void insertVertex(float x, float y, float z, int index)inside( ... )
bool inside(const T &p)Tests whether the T is within a closed ofPolyline.
Tests whether the ofPoint is within a closed ofPolyline.
inside( ... )
bool inside(float x, float y)Tests whether the x,y coordinates are within a closed ofPolyline.
Tests whether the x,y coordinates are within a closed ofPolyline.
isClosed( )
bool isClosed()lineTo( ... )
void lineTo(const T &to)Add a straight line from the last point added, or from 0,0 if no point is set, to the point indicated by the T passesd in.
Add a line from the last point added, or from 0,0 if no point is set, to the point indicated by the ofPoint passesd in.
lineTo( ... )
void lineTo(float x, float y, float z)Add a straight line from the last point added, or from 0,0 if no point is set, to the point indicated by the floats x,y,z passesd in.
Add a line from the last point added, or from 0,0 if no point is set, to the point indicated by the floats x,y,z passesd in.
ofPolyline_( )
ofPolyline_()Creates an ofPolyline.
Creates an ofPolyline.
operator[]( ... )
const T & operator[](int index)Allows you to access the points of the ofPolyline just like you would in an array, so to make the points of a line follow the mouse movement, you could do:
line[0].set(mouseX, mouseY);
int i = 1;
while ( i<bounds.size()) {
float angle = atan2(line[i-1].y - line[i].y, line[i-1].x - line[i].x);
bounds[i].set(bounds[i-1].x - cos(angle) * 20, bounds[i-1].y - sin(angle) * 20);
i++;
}
operator[]( ... )
T & operator[](int index)The [] operator allows you to access the points of the ofPolyline just like you would in an array, so to make the points of a line follow the mouse movement, you could do:
line[0].set(mouseX, mouseY);
int i = 1;
while ( i<bounds.size()) {
float angle = atan2(line[i-1].y - line[i].y, line[i-1].x - line[i].x);
bounds[i].set(bounds[i-1].x - cos(angle) * 20, bounds[i-1].y - sin(angle) * 20);
i++;
}
quadBezierTo( ... )
void quadBezierTo(const T &p1, const T &p2, const T &p3, int curveResolution=20)Adds a quadratic bezier line in 2D space from the current drawing point with the beginning indicated by the point p1, the control point at p2, and that ends at the point p3.
Creates a quadratic bezier line in 2D space from the current drawing point with the beginning indicated by the point p1, the control point at p2, and that ends at the point p3.
quadBezierTo( ... )
void quadBezierTo(float cx1, float cy1, float cx2, float cy2, float x, float y, int curveResolution=20)Adds a quadratic bezier line in 2D space from the current drawing point with the beginning indicated by the coordinates cx1, cy1, the control point at cx2, cy2, and that ends at the coordinates x, y.
Creates a quadratic bezier line in 3D space from the current drawing point with the beginning indicated by the coordinates cx1, cy1, the control point at cx2, cy2, and that ends at the coordinates x, y.
quadBezierTo( ... )
void quadBezierTo(float cx1, float cy1, float cz1, float cx2, float cy2, float cz2, float x, float y, float z, int curveResolution=20)Adds a quadratic bezier line in 3D space from the current drawing point with the beginning indicated by the coordinates cx1, cy1, cz1, the control point at cx2, cy2, cz2, and that ends at the coordinates x, y, z.

Creates a quadratic bezier line in 3D space from the current drawing point with the beginning indicated by the coordinates cx1, cy1, cz1, the control point at cx2, cy2, cz2, and that ends at the coordinates x, y, z.
resize( ... )
void resize(size_t size)Resize the number of points in the ofPolyline to the value passed in.
rotateDeg( ... )
void rotateDeg(float degrees, const glm::vec3 &axis)} \name Transform polyline {
rotateDeg( ... )
void rotateDeg(float degrees, const glm::vec2 &axis)rotateRad( ... )
void rotateRad(float radians, const glm::vec3 &axis)rotateRad( ... )
void rotateRad(float radians, const glm::vec2 &axis)scale( ... )
void scale(float x, float y)Change the size of the ofPolyline These changes are non-reversible, so for instance scaling by 0,0 zeros out all data.
setCircleResolution( ... )
void setCircleResolution(int res)}
setClosed( ... )
void setClosed(bool tf)Closes the ofPolyline, meaning that all the vertices will be linked and can be "walked".
setRightVector( ... )
void setRightVector(T v)simplify( ... )
void simplify(float tolerance=0.3f)Simplifies the polyline, removing un-necessary vertices.
Parameters:
tolerance determines how dis-similar points need to be to stay in the line. Higher tolerance means more points removed, lower tolerance means less points removed.
Simplifies the polyline, removing un-necessary vertices. The tolerance determines how dis-similar points need to be to stay in the line. Higher tolerance means more points removed, lower tolerance means less points removed.
size( )
size_t size()The number of points in the ofPolyline.
translate( ... )
void translate(const glm::vec3 &p)translate( ... )
void translate(const glm::vec2 &p)updateCache( ... )
void updateCache(bool bForceUpdate=false)wrapAngle( ... )
float wrapAngle(float angleRad)